在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球，若AB⊥BC，AB=6，BC=8，AA1=3，则V的最大值是()
- A.
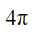
- B.
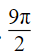
- C.
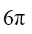
- D.
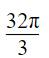
查看答案
纠错
若遇到问题请联系 客服QQ：3480655671
正确答案： B
本题解析：
由题意知，当球为直三棱柱的内接球时，体积最大，选取过球心且平行于直三棱柱底面的截面，如图所示，则由切线长定理可知，内接圆的半径为 2，
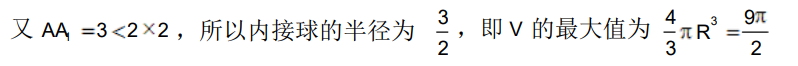
包含此试题的试卷
你可能感兴趣的试题
已知函数 f (x)=|2 x-a| +a
(Ⅰ)当 a=2 时，求不等式 f (x)≤6 的解集;
(Ⅱ)设函数 g(x)=|2 x-1| ，当 x∈R时，f (x)+g(x)≥3，求 a 的取值范围。
， 以坐标原点为极点，以 x 轴的正半轴为极轴，建立极坐标系，曲线 C2 的极坐标方程为 ρsin(＋θ π 4 )＝2√2.
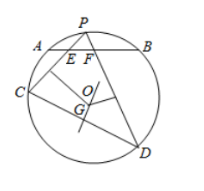
如图，⊙ O 中 ︵ AB 的中点为 P，弦 PC、PD 分别交 AB 于 E、F 两点。
（Ⅰ）若 ∠PFB＝2∠PCD，求∠PCD 的大小；
（Ⅱ）若 EC 的垂直平分线与 FD 的垂直平分线交于点 G，证明：OG ⊥CD.
设函数 f (x)=acos2x+(a-1)(cosx+1)，其中 a>0，记| f (x)| 的最大值为 A，
(Ⅰ)求 f '(x);
(Ⅱ)求 A;
(Ⅲ)证明 |f '(x)|≤2A
置顶