在直角坐标系 xOy中，曲线 C1的参数方程为 ， 以坐标原点为极点，以 x 轴的正半轴为极轴，建立极坐标系，曲线 C2 的极坐标方程为 ρsin(＋θ π 4 )＝2√2.

已知函数 f (x)=|2 x-a| +a

(Ⅰ)当 a=2 时，求不等式 f (x)≤6 的解集;

(Ⅱ)设函数 g(x)=|2 x-1| ，当 x∈R时，f (x)+g(x)≥3，求 a 的取值范围。

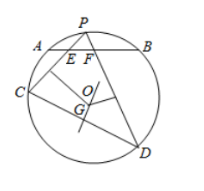
如图，⊙ O 中 ︵ AB 的中点为 P，弦 PC、PD 分别交 AB 于 E、F 两点。

（Ⅰ）若 ∠PFB＝2∠PCD，求∠PCD 的大小； 

（Ⅱ）若 EC 的垂直平分线与 FD 的垂直平分线交于点 G，证明：OG ⊥CD.

设函数 f (x)=acos2x+(a-1)(cosx+1)，其中 a>0，记| f (x)| 的最大值为 A，

(Ⅰ)求 f '(x);

(Ⅱ)求 A;

(Ⅲ)证明 |f '(x)|≤2A

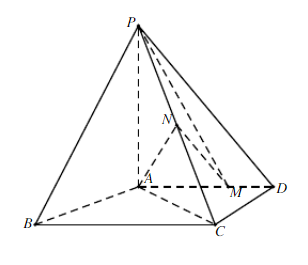
如图，四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点。

(Ⅰ)证明：MN∥平面PAB

(Ⅱ)求直线AN与平面PMN所成角的正弦值。点，AM=2MD，N为PC的中点。