设椭圆的焦点为F1(- √3,0),F2(√3,0), 其长轴长为4.
(I)求椭圆的方程:
(II) 设直线y=√3/2x+ m与椭圆有两个不同的交点,其中一个交点的坐标是(0,1),求另一个交点的坐标。
查看答案
纠错
若遇到问题请联系 客服QQ:3480655671
正确答案:
解:
( I )由己知,椭圆的长轴长2a=4,焦距2c=2√3,设其短半轴长为b,则.
b=√(a-c)=√(4-3)=1
所以椭圆的方程为-+y=1
( II )因为直线与椭圆的一个交点为(0,1) ,将该交点坐标代入直线方程可得m=1,
y=(√3/2)x+1
将直线与椭圆的方程联立得
解得另外一个交点坐标为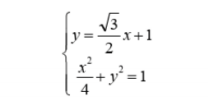
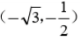
本题解析: 暂无解析
包含此试题的试卷
你可能感兴趣的试题
置顶