旋转变换在平面几何中有着广泛的应用.特别是在解(证)有关等腰三角形、正三角形、正方形等问题时, 更是经常用到的思维方法,请你用旋转交换等知识,解决下面的问题.
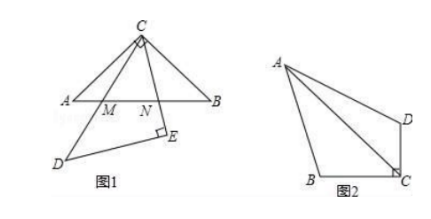
如图 1,△ABC与△DCE均为等腰直角三角形,DC与 AB交于点 M,CE与 AB交于点 N.
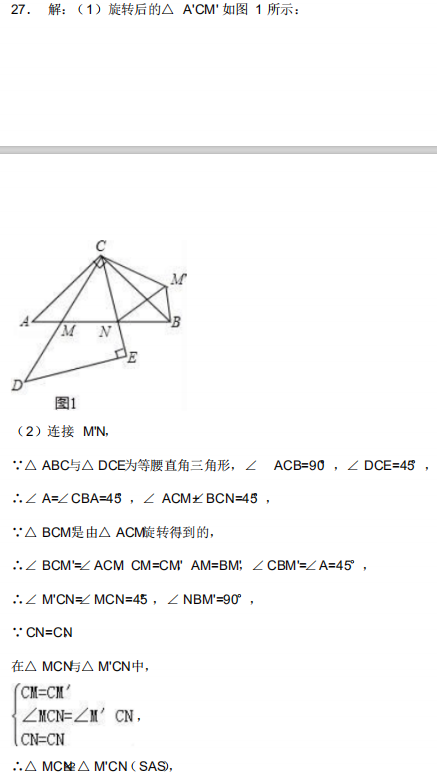
(1)以点 C为中心,将△ ACM逆时针旋转 90°,画出旋转后的△A′CM′
(2)在( 1)的基础上,证明AM2+BN2=MN2.
(3)如图 2,在四边形 ABCD中,∠ BAD=45°,∠ BCD=90°, AC平分∠ BCD,若 BC=4,CD=3,则对角线 AC的长度为多少? (直接写出结果即可,但在图中保留解决问题的过程中所作辅助线、标记的有关计算数据等)
查看答案
纠错
若遇到问题请联系 客服QQ:3480655671
正确答案:

本题解析: 暂无解析
包含此试题的试卷
你可能感兴趣的试题
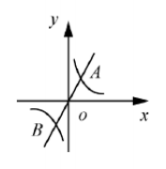
如题7图,在同一平面直角坐标系中,直线y=k1x(k1 0)与双曲线y=kz/x(k2 0)相交于A、B两点,已知点A的坐标为(1,2),则点B的坐标为()
- A. (-1,-2 )
- B. (-2,-1)
- C. (-1,-1 )
- D. (-2,-2 )
置顶