2019全国MBA联考综合能力真题及答案-解析
- 推荐等级：
- 发布时间：2020-05-07
- 卷面总分：110分
- 答题时间：120分钟
- 试卷题量：55题
- 练习次数：1491次
- 试卷分类：综合能力
- 试卷类型：历年真题
试卷预览
某车间计划 10 天完成一项任务，工作 3 天后事故停工 2 天，若仍要按原计划完成任务，则工作效率要提高 ( ).
- A. 20%
- B. 30%
- C. 40%
- D. 50%
- E. 60%
正确答案： C
本题解析：
整个工 程看做单位 "1" ， 原计划的工作 效 率 为 1/10 ， 实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50 ，因此工作效率提高了 (7/50-1/10)/(1/10)=40% ，选 C。
函数 f(x)=2x+a/ π2(a ﹥0) ，在 (0 ，+ ∞)内最小值为 f(x 0)=12 ，则 x0=
- A. 5
- B. 4
- C. 3
- D. 2
- E. 1
正确答案： B
本题解析：
利用三个数的均值定理求最值： a+b+c ≥3 3 √abc 。f(x)=2x+a/x 2 =x+x+a/x 2≥3 3√ x*x*a/x 2，因此最小值为 3 3√a=12 →a=64 ，因此 x=x=64/x 2→x=4 ，选 B。
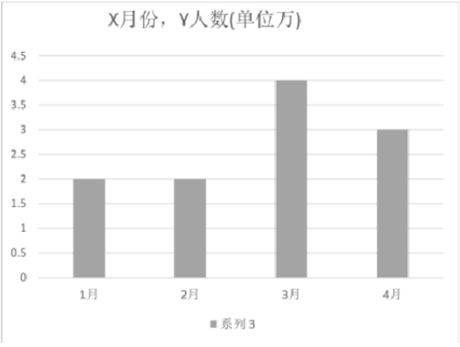
某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数为（）。
- A. 3:4
- B. 5:6
- C. 12:13
- D. 13:12
- E. 4:3
正确答案： C
本题解析：
如图可得：一季度男女观众人数分別为 :
男: 5w+ 4w+ 3w= 12w
女: 6w+ 3w+ 4w= 13w
故一季度男女人数比的 : 12:13 ，选 C。
没实数 a,b 満足 ab=6 ，|a+b| +|a-b|=6 ，则 a2+b2=( )
- A. 10
- B. 11
- C. 12
- D. 13
- E. 14
正确答案： D
本题解析：
ab=6, 特值法 a=2 ，b=3 満足条件， a2+b2=4+9=13 ，选 D。
设圆 C 与圆 (x-5) 2+y2=2 ，关于 y=2x 时称，则圆 C 方程为 ( )
- A. (x-3) 2 +(y-4) 2=2
- B. (x+4) 2 +(y-3) 2=2
- C. (x-3) 2 +(y+4) 2=2
- D. (x+3) 2 +(y+4) 2=2
- E. (x+3) 2 +(y-4) 2=2
正确答案： E
本题解析： 暂无解析
将一批树苗种在应该正方形花园边上，四角都种，如果每隔 3 米种一棵，那么剩下10课树苗 ,如果每隔 2 米种一棵那么种满正方形的 3 条边 ,则这批树苗有 ( ) 棵
- A. 54
- B. 60
- C. 70
- D. 82
- E. 94
正确答案： D
本题解析：
设正方形的边长为 x，由已知可得方程 4x/3+10=3x/2+1 ，求解得 x=54故树苗有 (54x4)/3+10=82 ，选 D。
在分别标记 1、2、3、4、5、6 的 6 张卡片里，甲抽取 1 张，乙从余下的卡片中再抽取2 张，乙的卡片的数字之和大于甲的卡片数字的概率为 ( )
- A. 11/60
- B. 13/60
- C. 43/60
- D. 47/60
- E. 49/60
正确答案： D
本题解析：
样本空间? =C16xC25；
事件 A：反面考虑，穷举法
甲抽 6，乙有 (5,1);(4,2);(4,1);(3,1);(3,2);(1,2) 共 6 种
甲抽 5，乙有 (4,1);(3,1);(3,2);(1,2) 共 4 种 ;
甲抽 4，乙有 (3,1);(1,2) 共 2 种 ，
甲抽 3，乙有 (1,2) 共 1 种
综上事件 A=6+4+2+1=13 种， 1-P(A)=1-13/(C 1 6+C 2 5 )=47/60 ，选 D 。
10 名同学的語文和数学成绩如下 :
语文成绩 : 90 、92 、94 、 88 、86 、85 、87 、89 、91 、93
数学成绩 : 94 、88 、96 、 93 、90 、85 、84 、80 、82 、98
语文和数学成绩的均値分別为 E1 和 E2,柝准差分別为 &1 和&2 ，则
- A. E1>E2, &1>&2
- B.
E1>E2, &1<&2 - C. E1>E2, &1=&2
- D.
E1<E2, &1>&2 - E.
E1<E2, &1<&28
正确答案： B
本题解析：
简化两組数据，以 90 为基数，如下 :
语文 : 0,2,4,-2,4,5,-3,-1,1,3 ， 平均值 : 5/10=0.5 ，故 E1=90.5
数学 : 4,-2,6,3,0,-5,-6,-10,-8,8, 平均值 : -1 ，故 E2=89
因此 : E1> E 2，观察两组数据的稳定性可知：语文较数学稳定，因此 &1>&2 ，选 B。
如图， 正方体于半径为 3m 球内， 且一面位于球的大圆上， 则正方体的表面积最大为 （）
- A. 12
- B. 18
- C. 24
- D. 30
- E. 36
正确答案： E
本题解析：
欲使正方体的表面积最大，正方体与球的位置关系如下图：
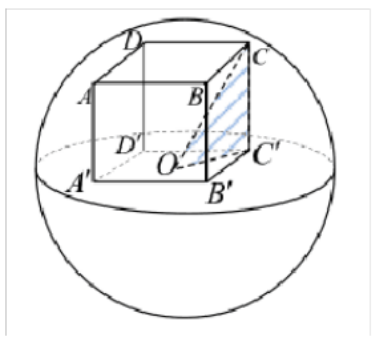
面 ABCD 在过球心的大圆上，点 A、B、C、D、在球面上球心 O 与球面上一点 C 连接即为 半径 : OC=3，在△OCC 中利用勾股定理，设正方体边长为 a，则 a 2 +( √2/2*a) 2 =3 2→a= √6，故正 方体表面积 S=6a 2 =36 ，选 E。
